音圧の問題
空気環境の調整16
音圧の問題
少し惑わされやすい問題に音圧レベルの問題があります。
ここで解説をいたします。
令和5年問題85
騒音レベル80dBと86dBの騒音を合成した場合の騒音レベルとして、最も近いものは次のうちどれか。
ただし、log102=0.3010、log103=0.4771、log105=0.6990とする。
- 83dB
- 86dB
- 87dB
- 89dB
- 166dB
答え【3】
この問題は対数log102=0.3010、log103=0.4771、log105=0.6990が記載されており、難しく感じると思いますが当サイトでは対数を使わないで問題を解きます。ポイントとしては以下に記載します。
- 対数計算は使わない。
- 騒音レベルの分解。
- ある法則により騒音レベルを求める。
ある法則により騒音レベルを求める。
- 同じ騒音レベルの機械を2台使用した場合は+3dBになる。
- 同じ騒音レベルの機械を4台使用した場合は+6dBになる。
- 同じ騒音レベルの機械を6台使用した場合は+8dBになる。
- 同じ騒音レベルの機械を8台使用した場合は+9dBになる。
- 同じ騒音レベルの機械を10台使用した場合は+10dBになる。
同じ騒音レベルの機械を2台使用した場合は+3dBになる。
騒音レベルの分解
騒音レベル80dBと86dBとあり
86dBを分解していきます。
上記記載した
同じ騒音レベルの機械を2台使用した場合は+3dBになる。
を利用して
86dBを分解していくと以下のようになります。
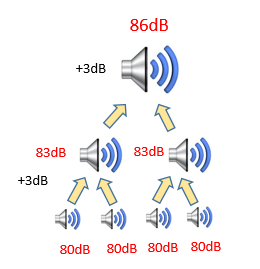
騒音レベル80dBと86dBの騒音を合成した場合の騒音レベルを合成したら以下のようになります。
騒音レベル80dBと86dB(80dB x 4dB)の騒音レベルと同じになり
結果として
騒音レベル80dBの機械を5台使用した場合の騒音レベルとなります。
- 同じ騒音レベルの機械を4台使用した場合は+6dBになる。
- 同じ騒音レベルの機械を6台使用した場合は+8dBになる。
4台のとき+6dB、6台のとき+8dBなので
5台のときは+7dBになりますので
答えは(3)の87dBになります。
平成24年 問題85
1台78dB(A)の騒音を発する機械を、測定点から等距離に6台同時に稼動させた場合の騒音レベルとして、最も近いものは次のうちどれか。ただし、log102=0.3010、log103=0.4771とする。
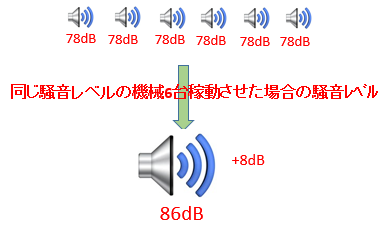
以下のような計算でも求められます。
X台運転したときの騒音レベルは、
+10log10Xで求めることが出来ます。つまり平成24年 問題85の場合だと、
6台同時に運転した場合なので +10log106になります。+10log10(2 x 3)
=10(log102 + log103)になります。
上記問題より
log102=0.3010、log103=0.4771
であるから
10(0.3010+0.4771)
=10 x 0.7781
=7.7781
になります。
つまり6台運転した場合の騒音レベルは+7.7781dB になり、
1台78dB(A)の騒音を発する機械を6台同時に稼動させた場合の騒音レベルは
78 + 7.7781 = 85.781dB
≒86dB
になります。
平成27年 問題86
騒音レベル83dBと92dBの騒音を合成した場合の騒音レベルとして、最も近いものは次のうちどれか。ただし、log102=0.3010、log103=0.4771とする。
まず、92dBの方を考えてみます。
同じ騒音レベルの機械を2台使用した場合は+3dBになる。
を逆に考えると
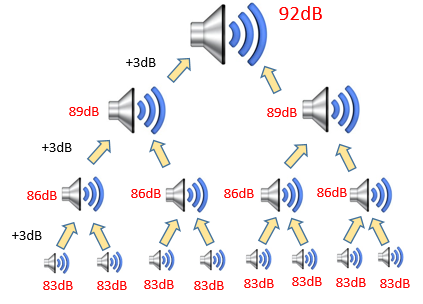
つまり、平成27年 問題86は
1台83dB(A)の騒音を発する機械を、9台同時に稼動させた場合の騒音レベルを求めることが出来る。と同じことになります。
同じ騒音レベルの機械を8台使用した場合は+9dBになる。
同じ騒音レベルの機械を10台使用した場合は+10dBになる。
つまり、9台の騒音レベルは+9dBと+10dBの間になる事から
83dB + 9dB = 92dB
83dB + 10dB = 93dB
になり、答えは92~93dB内になることが分かる。
答えは(4)92.5になります。
因みに 1台83dB(A)の騒音を発する機械を、9台同時に稼動させた場合の騒音レベルは
X台運転したときの騒音レベルは、
+10log10Xの公式より *10log109になり
+10log10(3 x 3)
=10(log103 + log103)になります。
問題文より
log103=0.4771ということなので
10 x (0.4771 + 0.4771) = 10 x 0.9542 = 9.542
になります。
従って答えは
83 + 9.542 = 92.542dB
正確に計算するとこのようになります。
ここでのポイントは、
- 2台稼働→+3dB
- 4台稼働→+6dB
- 6台稼働→+8dB
- 8台稼働→+9dB
- 10台稼働→+10dB
- X台運転したときの騒音レベルは
- +10log10X
X = a x b
より
+10log10(a x b)より
+10(log10a+log10b)
- +10log10X
面音源からの音圧レベルの伝搬特性に関する問題
この問題も数年に一度出題されますので簡単に解答できるポイントを掲載します。
令和6年問題85
面音源からの音圧レベルの伝搬特性に関する次の文章のに[ ]内に入る語句の組合せとして、最も適当なものはどれか。
下の図に示す寸法 α×b(α< b)の長方形の面音源について、面音源中心から面に対して垂直方向への距離を dとした場合、音源付近 d<b/πでは[ ア ]としの伝搬特性を示し、a/π < d < b/πでは線音源に対応する減衰特性を、d > b/πの範囲では[ イ ]に対応する減衰特性を示す。a/π < d < b/πの範囲で音源からの距離が 2倍になると[ ウ ]dB減衰する。

- (ア)点音源―――(イ)面音源―――(ウ)3
- (ア)点音源―――(イ)面音源―――(ウ)6
- (ア)面音源―――(イ)点音源―――(ウ)3
- (ア)面音源―――(イ)点音源―――(ウ)6
- (ア)面音源―――(イ)点音源―――(ウ)10
まず、ここで以下のこと覚えておきましょう。
- 面音源に近接した場所では減衰しない。
- 少し離れると線音源になり線音源の場合、音源からの距離が2倍になると音圧レベルは約3[dB]減衰する。
- 遠く離れると点音源になり点音源の場合、音源からの距離が2倍になると音圧レベルは約6[dB]減衰する。

長方形の面音源について、音源付近 d<b/πとあります。もうこの時点でアは音源付近なので面音源になることがわかります。
イにはd > b/πより一番遠く離れている部分なので点音源になります。
ウはa/π < d < b/πの範囲なので線音源になります。
線音源の場合、音源からの距離が2倍になると音圧レベルは約3[dB]減衰する。
ということなので3が入ります。
令和元年問題85
面音源からの音圧レベルの伝搬特性に関する次の文章の[ ]内に入る語句の組合せとして、最も適当なものはどれか。
「下の図に示す寸法a x b(a < b)の長方形の面音源について、面音源中心から面に対して垂直方向への距離をdとした場合、音源付近d < a/πでは[ ア ]としての伝搬特性を示し、a/π < d < b/πでは線音源に対応する減衰特性を、d > b/πの範囲では[ イ ]に対応する減衰特性を示す。よって、 d > b/πの範囲で音源からの距離が2倍になると[ ウ ]dB減衰する。」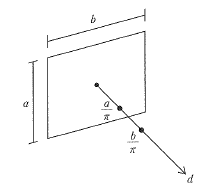
- (ア)点音源―――――(イ)面音源―――――(ウ)3
- (ア)点音源―――――(イ)面音源―――――(ウ)6
- (ア)面音源―――――(イ)点音源―――――(ウ)3
- (ア)面音源―――――(イ)点音源―――――(ウ)6
- (ア)面音源―――――(イ)点音源―――――(ウ)10
ほぼ令和6年問題85と同じ問題です。

点音源の場合、音源からの距離が2倍になると音圧レベルは約6[dB]減衰する。



